There are dozens of definitions of space depending on the context in which the word is used, but none is satisfactory to describe the nature of space.
The notion of space has evolved over time, the concept is linked to the history of mathematics and physics. For several millennia, intuitive and familiar, this concept has been expanded to become extremely complex.
How has evolved the notion of space over time until today?
For primitive peoples, the concept of space does not exist, according to ethnologists, the center of the world is the center of the village.
In ancient Greece, that of Pericles (around the year -495) space is a limited range occupied by the bodies. At the time of Plato (-428 -348) was born philosophy and science, and the concept of space is that of the void, the receptacle in which everything exists (Plato's Timaeus). For Aristotle (-384 -322), the space is the sum of the places. The first formal classical notion of space, emerges with the geometry of Euclid (around -300). Space is "geometrized".
During the Islamic Golden Age (≈1250 to ≈750) and until the end of the Middle Ages, the concept of space is that of Euclid. The Islamic Golden Age began with the translation of scientific works of Greek origins, Indian, Persian and Syriac, to Arabic.
During the Renaissance, the space becomes more abstract, it is modified by painters who trace in their paintings, projections on a plane, projective geometry appears.
In the 17th century comes the Newtonian revolution which marks the beginning of modern science. | | Newton express the properties of a physical space and a physical time. Therefore, all phenomena will take place in a space unchangeable, absolute, and in a time that always flows in the same direction.
Today in black holes, space and time merge.
The space has evolved from a philosophical concept to a mathematical and physical concept.
Currently, the space refers to the geometry, time itself geometrized is the fourth dimension of space. The time represented as the continuous succession of moments on a straight line, is a one-dimensional space.
The special relativity of Einstein combines these two entities as spacetime, a four-dimensional space.
In Euclidean geometry objects are idealized. The point, right, polyhedron, conic sections and their measures are length, area, volume, appear in an intuitive space.
Today the Euclidean straight line became a mathematical manifold of one-dimensional, plane a manifold of two-dimensional, Euclidean space a manifold of three dimensions. These three manifold are part of other mathematical manifolds of n-dimensions.
These are the 19th century mathematicians such as Carl Friedrich Gauss (1777-1855), Bernhard Riemann (1826-1866), János Bolyai (1802-1860), Johann Heinrich Lambert (1728-1777), who showed that besides this Euclidean space, there were others n-dimensional spaces.
At that time an additional property is attributed to the space. | |  Image: The Flagellation of Christ by Piero Della Francesca (between 1444 and 1478). The work of Piero Della Francesca, master of perspective and Euclidean geometry, also reproduced perfectly as possible the space taken up by the human eye. From the beginning of the renaissance space becomes more abstract, can be seen from the outside.
The synthetic Euclidean geometry then presents a problem, in particular, the axiom of parallels (Euclid's fifth postulate). |
At the end of the 19th century, developments in mathematics will lead to redefine the notion of space.
The space now has a curvature, zero, positive or negative and can vary from one point to another in space. For example, the straight line and the plane have a constant curvature equal to zero, the sphere has a constant curvature equal to 1/R2, in other words the curvature of the sphere is greater as the radius is small.
But the curvature is not simply described as a number but by a tensor, a complex mathematical object that can vary from one place to another in space.
Bumpy surfaces have a curvature at each point as the surface of an ocean at each location there is a different curvature.
In the 20th century Einstein adds time to space.
The concept of spacetime was introduced by Hermann Minkowski (1864−1909) in 1908 in a mathematical presentation on the geometry of space and time as it was defined by the theory of relativity of Albert Einstein (1877−1953).
Spacetime is a 4-dimensional manifold that has a variable curvature from one place to another. This curvature is gravitation. All objects in the space feel this curvature. "So between Earth and the Moon there is geometry."
The differential geometry of Bernhard Riemann (1826−1866) will pave the way for non-Euclidean geometries, which will allow Einstein to develop the theory of General Relativity that identifies the gravitational effects on the curvature of space. Therefore, the global topology of the space will be the subject of much research. Mathematicians are still complicate the notion of space. The space now has n dimensions, plus it is multiple, each space belongs to a class of space and the curvature exists in all spaces. | | The other innovation of space is expressed by the non-commutative geometry developed by Alain Connes in 1985. In a non-commutative space, the notion point disappears, the very nature of space prohibits locating a particle. With quantum mechanics, a microscopic system, an atom for example, has coordinates, such as position, which no longer commute. In these spaces, the algebra of coordinates no longer obeys the commutative rule (x + y = y + x).
When you want to know where there is a particle results in an uncertainty relation. The position of the particle can not be located in the space with precision.
In 1924, Louis Victor de Broglie (1892−1987) asserts that any matter has an associated wave. The space of the particle depends on the temperature, that is the famous wavelength of de Broglie.
Then come the fiber spaces and the concept of neighborhood, of projection and connection.
This is a separate space (fiber) supported on another space (base) where each point of the base accepts a neighbor, all connected by a series of "cards" which commute. The representation is not at all intuitive. One type of fiber space is given by the Möbius strip (see picture).
Since 2500 years, we have expanded the concept of space to Euclidean geometry, non-Euclidean manifolds, non commutative geometry pasting to quantum physics then to fiber spaces pasting to quantum physics fields, but scientists have not yet found a unified theory of space and time that works in two worlds, that of the subatomic world and the macroscopic world.
It is quite possible that the notions of space and time do not exist but only appear when our eyes interpret the world around us. | |  Image: It is easy to visualize the Möbius strip in space. It is a simple model to achieve, just do a twist to a strip of paper and then pasting its two ends. And there can be seen that the tape has only one side, unlike a conventional tape which has two. Mobius strip provided of the projection on a mediator circle is a fiber space. This is a simple example of abstract manifold but beyond two dimensions this is no longer representable. Thus the Klein bottle, a closed surface without boundary and not adjustable in 3-dimensional space, has no "inside" or "outside".
credit: GNU Free Documentation License |



 Automatic translation
Automatic translation

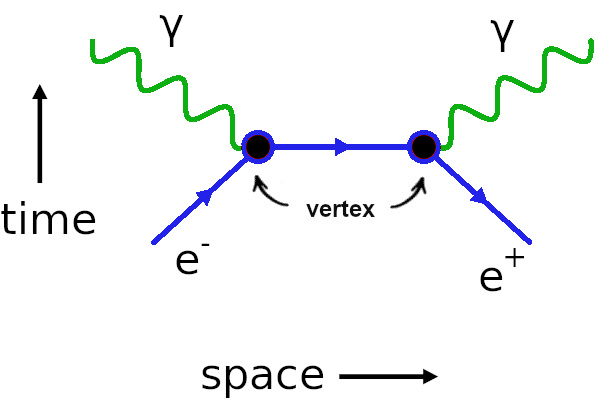 Feynman diagrams and particle physics
Feynman diagrams and particle physics
 Stars cannot create elements heavier than iron because of the nuclear instability barrier
Stars cannot create elements heavier than iron because of the nuclear instability barrier
 What is β radioactivity?
What is β radioactivity?
 Planck wall theory
Planck wall theory
 Is emptiness really empty?
Is emptiness really empty?
 The Large Hadron Collider
The Large Hadron Collider
 The hadron is not a fixed object
The hadron is not a fixed object
 Radioactivity, natural and artificial
Radioactivity, natural and artificial
 The scale of nanoparticles
The scale of nanoparticles
 Schrodinger's Cat
Schrodinger's Cat
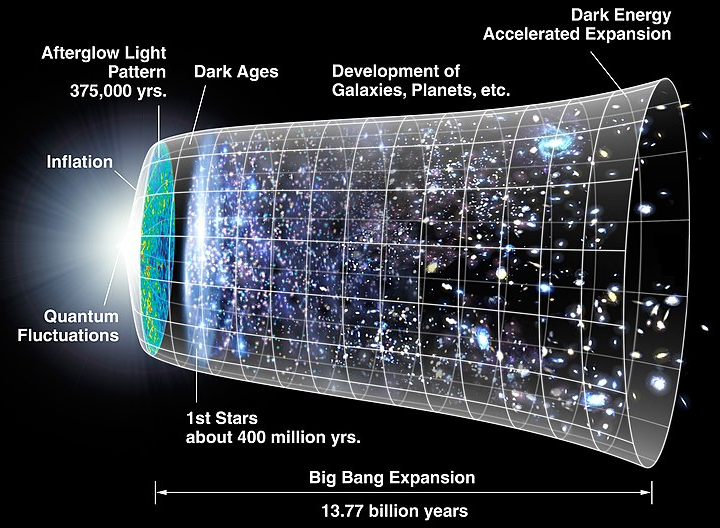
 Before the big bang the multiverse
Before the big bang the multiverse
 Eternal inflation
Eternal inflation
 Gravitational waves
Gravitational waves
 Principle of absorption and emission of a photon
Principle of absorption and emission of a photon
 Beyond our senses
Beyond our senses
 What is a wave?
What is a wave?
 The fields of reality: what is a field?
The fields of reality: what is a field?
 Space in time
Space in time
 Quantum computers
Quantum computers
 Bose-Einstein condensate
Bose-Einstein condensate
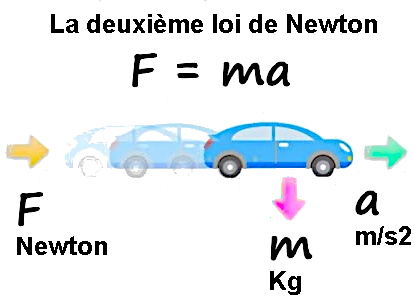 Equation of Newton's three laws
Equation of Newton's three laws
 Field concept in physics
Field concept in physics
 The electron, a kind of electrical point
The electron, a kind of electrical point
 Entropy and disorder
Entropy and disorder
 Light, all the light of the spectrum
Light, all the light of the spectrum
 The infernal journey of the photon
The infernal journey of the photon
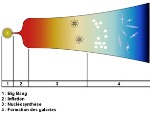 Mystery of the Big Bang, the problem of the horizon
Mystery of the Big Bang, the problem of the horizon
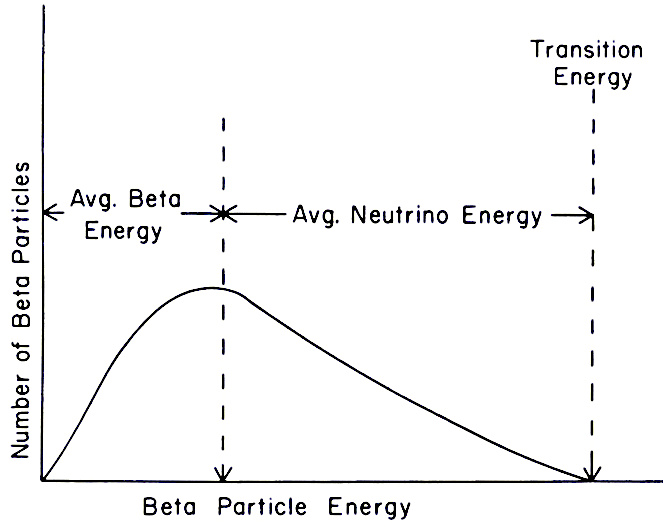
 The neutrino and beta radioactivity
The neutrino and beta radioactivity
 Einstein's space time
Einstein's space time
 The incredible precision of the second
The incredible precision of the second
 Why does physics have constants?
Why does physics have constants?
 Spectroscopy, an inexhaustible source of information
Spectroscopy, an inexhaustible source of information
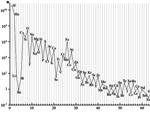 Abundance of chemical elements in the universe
Abundance of chemical elements in the universe
 Effects of light aberration
Effects of light aberration
 The size of atoms
The size of atoms
 The magnetic order and magnetization
The magnetic order and magnetization
 The quark confinement
The quark confinement
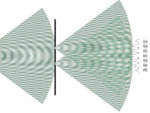 Superpositions of quantum states
Superpositions of quantum states
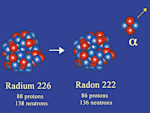 Alpha decay (α)
Alpha decay (α)
 Electromagnetic induction equation
Electromagnetic induction equation
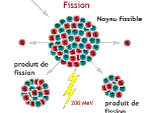 Nuclear fusion, natural energy source
Nuclear fusion, natural energy source
 Does dark matter exist?
Does dark matter exist?
 Non-baryonic matter
Non-baryonic matter
 The mystery of the structure of the atom
The mystery of the structure of the atom
 The mystery of matter, where mass comes from
The mystery of matter, where mass comes from
 Nuclear energy and uranium
Nuclear energy and uranium
 The Universe of X-rays
The Universe of X-rays
 How many photons to heat a coffee?
How many photons to heat a coffee?
 Image of gold atom, scanning tunneling microscope
Image of gold atom, scanning tunneling microscope
 Quantum tunneling of quantum mechanics
Quantum tunneling of quantum mechanics
 Entropy and its effects, the passage of time
Entropy and its effects, the passage of time
 The 12 particles of matter
The 12 particles of matter
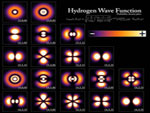 The atomic orbital or image atom
The atomic orbital or image atom
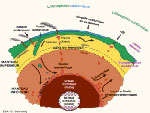 Earth's radioactivity
Earth's radioactivity
 The Leap Second
The Leap Second
 The vacuum has considerable energy
The vacuum has considerable energy
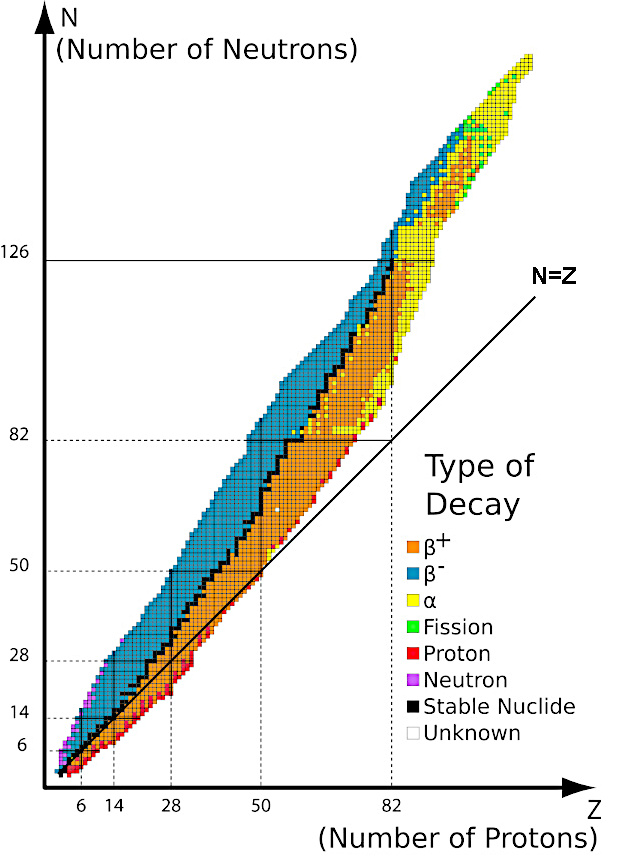
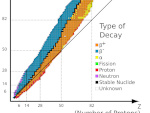 The valley of stability of atomic nuclei
The valley of stability of atomic nuclei
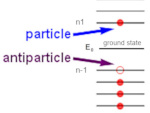 Antimatter and antiparticle
Antimatter and antiparticle
 What is an electric charge?
What is an electric charge?
 Our matter is not quantum!
Our matter is not quantum!
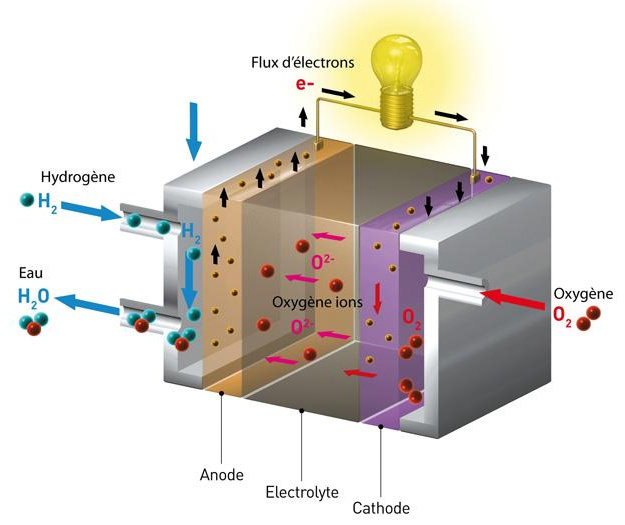 Why use hydrogen in the fuel cell?
Why use hydrogen in the fuel cell?
 The secrets of gravity
The secrets of gravity
 E=mc2 explains the mass of the proton
E=mc2 explains the mass of the proton
 Image of gravity since Albert Einstein
Image of gravity since Albert Einstein
 Einstein's miraculous year: 1905
Einstein's miraculous year: 1905
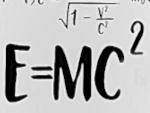 What does the equation E=mc2 really mean?
What does the equation E=mc2 really mean?
 Special relativity and space and time
Special relativity and space and time