Todos los aglomerados de un cuerpo celeste se mantienen unidos por su propia gravedad.
El límite de Roche o radio de Roche es la distancia a la que un pequeño cuerpo celeste se desintegrará debido a las fuerzas de marea de otro cuerpo celeste, cuya fuerza de atracción excede la auto-atracción del pequeño cuerpo. En otras palabras, el límite de Roche es la distancia mínima desde el centro del planeta, que permite que el material se unen para formar, por ejemplo, una luna lo suficientemente grande.
De hecho las fuerzas de marea prohíben la formación de un cuerpo masivo cerca del planeta. Una cierta distancia es necesario para que el polvo y los pequeños desechos « pegarse » y forman un objeto muy masivo. Esta distancia se llama el límite de Roche del matemático y astrónomo francés Édouard Albert Roche (1820-1883), que calcula el límite teórico en 1848.
Por debajo de este límite, un objeto empieza a romper como la acción de las fuerzas de marea es mayor que las fuerzas de cohesión de los materiales que constituyen el objeto.
Más allá de este límite, las fuerzas de marea no producen sólo la fricción entre los materiales del satélite y del planeta. Esto por lo general produce una protuberancia en la superficie de los objetos.
Se conoce, el límite de Roche para los cuerpos rígidos, se encuentra para dos cuerpos de misma densidad ≈ 2,42 veces el radio del planeta. Para los cuerpos fluidos, se encuentra para dos cuerpos de misma densidad ≈ 1,26 veces el radio del planeta.
Tabla : distancia de los anillos en el sistema solar en relación con el límite de Roche.
¿Cómo se lee este tabla?
El anillo de Saturno es 1,44 veces el límite de Roche de cuerpos rígidos y 0,75 veces, es decir, en el interior del límite de Roche de cuerpos fluidos. Los anillos por definición, no son rígidos y se consideran como cuerpos fluidos. Los aglomerados de polvo y piedras no podrán ensamblarse porque la fuerza de marea de Saturno evitará todo « atraerse ». Cálculos realizados por astronoo.com | | | Closest rings | Roche limit
(rigid) | Roche limit
(fluid) | | | number of
Roche radius | number of
Roche radius | |
| | | | A ring (Saturn) | 1.44 | 0.75 | | B ring (Saturn) | 1.08 | 0.56 | | C ring (Saturn) | 0.88 | 0.46 | | D ring (Saturn) | 0.79 | 0.41 | | E ring (Saturn) | 2.13 | 1.11 | | F ring (Saturn) | 1.65 | 0.86 | | G ring (Saturn) | 2.00 | 1.04 | | Halo ring (Jupiter) | 1.49 | 0.78 | | Main ring (Jupiter) | 1.75 | 0.91 | Amalthea gossamer
ring (Jupiter) | 2.17 | 1.13 | Thebe gossamer
ring (Jupiter) | 2.48 | 1.29 | | ζcc (Uranus) | 0.69 | 0.36 | | ζc (Uranus) | 0.81 | 0.42 | | 1986U2R (Uranus) | 0.85 | 0.44 | | ζ (Uranus) | 0.88 | 0.46 | | 6, 5 and 4 rings (Uranus) | 0.93 | 0.49 | | α (Uranus) | 1.00 | 0.52 | | β (Uranus) | 1.02 | 0.53 | | η (Uranus) | 1.05 | 0.55 | | γ (Uranus) | 1.06 | 0.55 | | δ (Uranus) | 1.08 | 0.56 | | Galle (Neptune) | 0.90 | 0.47 | | Le Verrier (Neptune) | 1.14 | 0.59 | | Lassell (Neptune) | 1.18 | 0.62 | | Arogo (Neptune) | 1.23 | 0.64 | | Adams (Neptune) | 1.35 | 0.70 |
| |  Imagen: El campo de gravedad de la pequeña luna crea ondas oscuras visibles en esta imagen del anillo F. Los anillos de Saturno (A, B, C, D, E, F, G) se encuentran dentro o cerca del límite de Roche para los cuerpos fluidos. Prometeo y Pandora están dentro del límite de Roche para los cuerpos fluidos, pero más allá del límite de Roche para los cuerpos rígidos. En esta imagen vemos Prometeo crear corrientes extrañas en el anillo F de Saturno. Esta pequeña luna gira alrededor de Saturno dentro del fino anillo F y se acerca del borde interior del anillo cada 15 horas. El bajo campo de gravedad de Prometeo atrae las finas partículas de polvo hielo alrededores, provocando ondas oscuras, falta de material. Prometeo crea un nuevo flujo a cada paso, por lo que a veces varios de ellos son visibles al mismo tiempo. crédito de la Imagen: Cassini Imaging Team, ISS, JPL, ESA, NASA N.B.: Alrededor de los planetas del sistema solar dentro del límite de Roche, sólo hay anillos o muy pequeños cuerpos pocos masivos. |
¿Cómo calcular el límite de Roche para los cuerpos rígidos?
Límite de Roche para los cuerpos rígidos :
d= 2.422849865 x R x 3√ρM/ρm
d = límite de Roche
R = radio del planeta
ρM = densidad o masa volúmica del planeta
ρm = densidad o masa volúmica de la luna
fórmula de Excel para el cálculo :
=(2.422849865*R)*(ρM/ρm)^(1/3)
¿Cómo calcular el límite de Roche para los cuerpos fluidos?
Límite de Roche para los cuerpos fluidos :
d = 1.26 x R x 3√ρM/ρm
fórmula de Excel para el cálculo :
=(1.26*R)*(ρM/ρm)^(1/3)
Las fuerzas de marea ejercidas por el planeta reducen la velocidad lentamente del satélite, cuando está dentro del límite de Roche. La luna está perdiendo poco a poco la altitud y puede dislocarse alcanzando el límite de Roche y de este modo formar un nuevo anillo planetario. Por el contrario, más allá del límite de Roche, las fuerzas de marea aceleran muy lentamente el satélite y lo aleje, es el caso de la Luna que se aleje de la Tierra de 3,78 cm por año. Sin embargo, varias lunas en el sistema solar están peligrosamente cerca de la límite de Roche su planeta, su final de la vida se ha programado. Si no se dislocan acercándose de la límite de Roche, van a encender en la atmósfera de su planeta. Este es particularmente el caso de Phobos (luna de Marte), Amalthea (luna de Júpiter), Prometeo y Pandora (luna de Saturno), Cordelia y Ofelia (lunas de Urano) y Galatea, Thalassa, Despina o náyade (luna Neptuno).
N.B.: La densidad, o más precisamente, la densidad de la masa volúmica de una sustancia es la masa por unidad de volumen. El símbolo más utilizado para la densidad es ρ (la letra griega rho). Matemáticamente, la densidad se define como el peso dividido por el volumen. | | | Moons near the limits | Roche limit
(rigid) | Roche limit
(fluid) | | | number of
Roche radius | number of
Roche radius | | | | | | Phobos (Mars) | 1.72 | 0.89 | | Amalthea (Jupiter) | 1.74 | 0.91 | | Thebe (Jupiter) | 2.13 | 1.11 | | Metis (Jupiter) | 1.23 | 0.64 | | Adrastea (Jupiter) | 1.24 | 0.64 | | Prometheus (Saturn) | 1.63 | 0.85 | | Pandora (Saturn) | 1.67 | 0.87 | | Mimas (Saturn) | 2.90 | 1.51 | | Cordelia (Uranus) | 1.54 | 0.80 | | Ophelia (Uranus) | 1.66 | 0.86 | | Bianca (Uranus) | 1.83 | 0.95 | | Cressida (Uranus) | 1.91 | 0.99 | | Desdemona (Uranus) | 1.94 | 1.01 | | Juliet (Uranus) | 1.99 | 1.03 | | Portia (Uranus) | 2.04 | 1.06 | | Larissa (Neptune) | 2.12 | 1.11 | | Galatea (Neptune) | 1.53 | 0.80 | | Despina (Neptune) | 1.52 | 0.79 | | Thalassa (Neptune) | 1.45 | 0.75 | | Naiad (Neptune) | 1.43 | 0.74 |
Tabla : distancias (semieje mayor) de las lunas más cercanas de la límite de Roche de sus planetas.
¿Cómo se lee este gráfico?
Fobos, la luna de Marte es 1,72 veces el límite de Roche de los cuerpos rígidos y 0.89 veces, es decir, dentro del límite de Roche de los cuerpos fluidos. Las lunas son cuerpos rígidos, que fueron capaces de ensamblarse porque la fuerza de las mareas en este punto es más bajo que su propia gravedad. | | 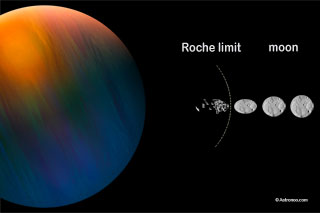 Imagen: Cuando la Luna está cerca del límite de Roche, las fuerzas de marea ejercidas por el planeta, reducen la velocidad lentamente. La luna está perdiendo poco a poco la altitud y puede dislocarse alcanzando el límite de Roche, es un escenario posible para la formación de anillos planetarios. Aunque el origen del anillo planetario no se conoce con certeza, hay tres escenarios.
1) Los anillos planetarios se forman al inicio, a partir del material del disco protoplanetario. El material que está en el límite de Roche del planeta, no se puede reunirse para formar lunas.
2) Los anillos planetarios se forman a partir de los restos de una luna que fue golpeado por otro objeto.
3) Los anillos planetarios se forman a partir de los restos de una luna que fue destruida por las fuerzas de marea dentro del límite de Roche del planeta.
Crédito Imagen: astronoo.comN.B.: el límite de Roche lleva el nombre del matemático y astrónomo francés Édouard Albert Roche (1820-1883). El límite de Roche tiene un campo similar en la Galaxia : el radio de marea. |
 Traducción automática
Traducción automática




 Los objetos más grandes del sistema solar
Los objetos más grandes del sistema solar
 Luna de la Tierra
Luna de la Tierra
 Fobos chocará contra Marte
Fobos chocará contra Marte
 Europa luna de Júpiter
Europa luna de Júpiter
 io luna de Júpiter
io luna de Júpiter
 Jápeto luna de Saturno
Jápeto luna de Saturno
 Dione luna de Saturno
Dione luna de Saturno
 Mimas luna de Saturno
Mimas luna de Saturno
 Teoría del impacto detrás de la Luna
Teoría del impacto detrás de la Luna
 Las lunas de Neptuno
Las lunas de Neptuno
 Eclipse lunar, concordancia celeste
Eclipse lunar, concordancia celeste
 Plutón y sus satélites
Plutón y sus satélites
 Los grandes cráteres de la Luna
Los grandes cráteres de la Luna
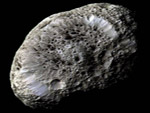 Hiperión, luna de Saturno
Hiperión, luna de Saturno
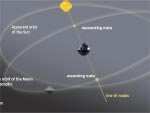 Eclipses explicados por el plano de la órbita lunar
Eclipses explicados por el plano de la órbita lunar
 Titán y Dione vistos por Cassini
Titán y Dione vistos por Cassini
 Erupciones de géiseres de hielo en Encelado
Erupciones de géiseres de hielo en Encelado
 Amaltea, un remanente de un bloque de Júpiter
Amaltea, un remanente de un bloque de Júpiter
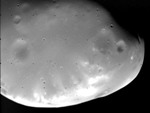 Deimos luna de Marte
Deimos luna de Marte
 Ilusión de la gran luna
Ilusión de la gran luna
 La pequeña Rea, muy cerca de Saturno
La pequeña Rea, muy cerca de Saturno
 Helena, la pequeña luna troyana de Saturno
Helena, la pequeña luna troyana de Saturno
 Titania luna de Urano
Titania luna de Urano
 La luna azul
La luna azul
 Cráter Stickney en Fobos
Cráter Stickney en Fobos
 Caronte, la gran luna de Plutón
Caronte, la gran luna de Plutón
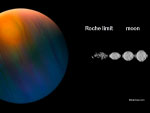 Límite de Roche o límite que no debe superarse
Límite de Roche o límite que no debe superarse
 Súper luna
Súper luna
 Lunas del sistema solar
Lunas del sistema solar
 Ganímedes, la luna más grande de Júpiter
Ganímedes, la luna más grande de Júpiter
 Tetis luna de Saturno
Tetis luna de Saturno
 Titán, luna de Saturno
Titán, luna de Saturno
 2 lunas nuevas para Júpiter
2 lunas nuevas para Júpiter
 Prometeo, el satélite pastor
Prometeo, el satélite pastor
 Tritón, la luna más grande de Neptuno
Tritón, la luna más grande de Neptuno
 Miranda luna de Urano
Miranda luna de Urano
 Tránsito de la Luna frente al Sol
Tránsito de la Luna frente al Sol
 Los mascones o anomalías gravitacionales de la Luna
Los mascones o anomalías gravitacionales de la Luna