fr en es
astronomie
 
Contacter l'auteur rss astronoo
Astéroïdes et Comètes Constellations Eclipses Environnement Etoiles Enfants Evolution Exoplanetes Galaxies Lumiere Lunes Matière Nébuleuses Planètes et planètes naines Soleil Sondes et télescopes Terre Trous noirs Univers Volcans Zodiaque Nouveaux articles Autres articles
 
 
 
 
 
 

Masse de Jupiter

Calcul de la masse de Jupiter

    
On se propose de déterminer la masse de Jupiter en étudiant le mouvement de ses principaux satellites : Io, Europe, Ganymède et Callisto.
Le mouvement d'un satellite, de masse m est étudié dans un référentiel considéré comme galiléen, ayant son origine au centre de Jupiter et ses axes dirigés vers des étoiles lointaines, considérées comme fixes. On supposera que Jupiter et ses satellites ont une répartition de masse à symétrie sphérique. Le satellite se déplace sur une orbite circulaire, à la distance R du centre de Jupiter :
- Déterminer la nature du mouvement d'un satellite autour de Jupiter.
- Déterminer la vitesse v d'un satellite en fonction de R, de M, masse de Jupiter et de G, constante de gravitation universelle.
- En déduire l'expression de la période de révolution T du satellite.
- Montrer que le rapport T2/ R3 est constant.

Les périodes de révolution et les rayons des orbites des quatre principaux satellites de Jupiteront été déterminés et ont les valeurs suivantes :

 IoEuropeGanymèdeCallisto
T(en heures)42,585,2171,7400,5
R(en km)4,22 1056,71 1051,07 1061,883 106

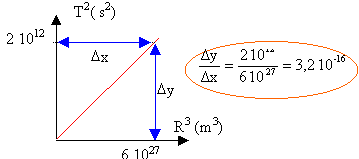
- Représenter sur papier millimétré le graphe donnant les variations de T² en fonction de R3. Conclure.
- En reliant ces résultats à ceux obtenus ci-dessus, déterminer la masse M de Jupiter.
donnée : G = 6,67 fois 10-11N.m2.kg-2.

Corrigé

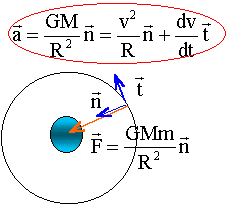
Le satellite est soumis à la seule force de gravitation centripète

masse de Jupiter

dans la base de Frenet : suivant l'axe n = GMm /R² = mv²/ (R+h) d'où la vitesse : v² =GM / R
suivant l'axe t : dv/dt = 0 d'où norme de la vitesse constante et mouvement uniforme.
la circonférence du cercle 2πR est parcourue à la vitesse v pendant la durée T (période 2πR =vT)
élever au carré et remplacer v² par son expression 4²R²= GM / R T²
soit T²/ R3 = 4²/(GM)(3ème loi de Kepler).

T² en fonction de (R+h) au cube donne une droite dont le coefficient directeur est 4pi²/GM

 IoEuropeGanymèdeCallisto
T(en secondes)1,53 1053,07 1056,18 1051,44 106
R(en m) 4,22 1086,71 1081,07 1091,883 109
T² en s²2,34 10109,42 10103,81 10112,07 1012
R3 en m37,51 10253 10261,22 10276,64 1027
T² / R33,1 10-163,14 10-163,12 10-163,2 10-16


T² / R3 est à peu près constant et égal à : 3,15 10-16. 
La 3ème loi de Kepler est bien vérifiée.

masse de Jupiter

Masse de Jupiter : T² / R3 = 4²/(GM)(3ème loi de Kepler).
M = 4p² / ( 3,15 10-16 * 6,67 10-11) = 1,87 * 1027 kg.

Les plus gros objets du système solaire Les plus gros objets du système solaire
Lune de la Terre Lune de la Terre
Phobos, s'écrasera sur Mars Phobos, s'écrasera sur Mars
Europe, lune de Jupiter Europe, lune de Jupiter
Io, lune de Jupiter Io, lune de Jupiter
Japet, lune de Saturne Japet, lune de Saturne
Dioné, lune de Saturne Dioné, lune de Saturne
Mimas, lune de Saturne Mimas, lune de Saturne
Théorie de l'impact à l'origine de la Lune Théorie de l'impact à l'origine de la Lune
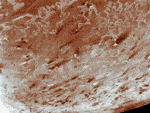Les lunes de Neptune Les lunes de Neptune
Éclipse de Lune, concordance céleste Éclipse de Lune, concordance céleste
Pluton et ses satellites Pluton et ses satellites
Les grands cratères de la Lune Les grands cratères de la Lune
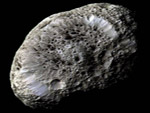Hypérion lune de Saturne Hypérion, lune de Saturne
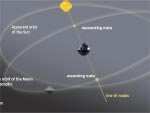Eclipses expliquées par le plan de l'orbite lunaire Eclipses expliquées par le plan de l'orbite lunaire
Titan et Dioné vus par cassini Titan et Dioné vus par cassini
Éruptions de geysers de glace sur Encelade Éruptions de geysers de glace sur Encelade
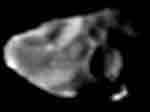Amalthée, un reste de bloc de Jupiter Amalthée, un reste de bloc de Jupiter
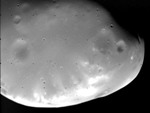Deimos, lune de Mars Deimos, lune de Mars
Illusion de la grande Lune Illusion de la grande Lune
La petite Rhéa, très proche de Saturne La petite Rhéa, très proche de Saturne
Hélène, la petite lune troyenne de Saturne Hélène, la petite lune troyenne de Saturne
Titania, lune d'Uranus Titania, lune d'Uranus
La Lune bleue La Lune bleue
Cratère Stickney sur Phobos Cratère Stickney sur Phobos
Charon la grande lune de Pluton Charon la grande lune de Pluton
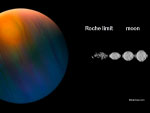Limite de Roche ou limite à ne pas dépasser Limite de Roche ou limite à ne pas dépasser
Super Lune Super Lune
Les lunes du système solaire Les lunes du système solaire
Ganymède, la plus grosse lune de Jupiter Ganymède, la plus grosse lune de Jupiter
Tethys lune de Saturne Tethys lune de Saturne
Titan lune de Saturne Titan lune de Saturne
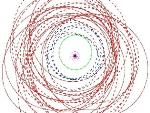2 nouvelles lunes pour Jupiter 2 nouvelles lunes pour Jupiter
Prométhée, le satellite berger Prométhée, le satellite berger
Triton, la plus grosse lune de Neptune Triton, la plus grosse lune de Neptune
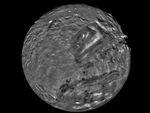Miranda lune d'Uranus Miranda lune d'Uranus
Transit de la Lune devant le Soleil Transit de la Lune devant le Soleil
Les mascons ou anomalies gravitationnelles de la Lune Les mascons ou anomalies gravitationnelles de la Lune
1997 © Astronoo.com − Astronomie, Astrophysique, Évolution et Écologie.
"Les données disponibles sur ce site peuvent être utilisées à condition que la source soit dûment mentionnée."

Contact −  Mentions légales −  Sitemap −  Comment Google utilise les données