Mass of Jupiter | |||||||||||||||||||
Calculation of the mass of Jupiter |  Automatic translation Automatic translation | Updated June 01, 2013 | |||||||||||||||||
We suggest determining the mass of Jupiter by studying the movement of its main satellites: Io, Europe, Ganymede and Callisto. The movement of a satellite, a mass m is studied in repository one considered as Galilean, having his origin in the center of Jupiter and its axes steered towards distant stars, considered as fixed .On will suppose that Jupiter and its satellites have a distribution of mass in a spherical symmetry. The satellite moves on a circular orbit, at the distance R of the center of Jupiter: The periods of revolution and beams of the orbits of four main satellites of Jupiter were determined and have the following values:
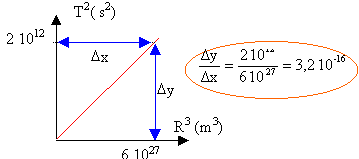
- Represent on graduated paper the graph giving the variations of T² According to R3. Conclude. data: G = 6,67 times 10-11N.m2.kg-2. | |||||||||||||||||||
Correction | |||||||||||||||||||
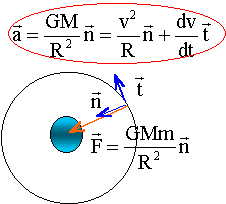
The satellite is subjected to the only strength of centripetal gravitation
In the base of Frenet: according to the axis n = GMm /R² = mv²/ (R+h) where from the speed: v² =GM / R T² According to (R+h) in the cube give a right the guiding coefficient of which is 4pi²/GM
Mass of Jupiter: T² / R3 = 4p²/(GM) (3rd law of Kepler). | ||||||||||||||||||||||||||||||||||
Result | ||||||||||||||||||||||||||||||||||
| M = 4p² / ( 3,15 10-16 *6,67 10-11) = 1,87 1027 kg. | ||||||||||||||||||||||||||||||||||
"The data available on this site may be used provided that the source is duly acknowledged."



 The largest objects in the solar system
The largest objects in the solar system
 The Moon of the earth
The Moon of the earth
 Phobos, will crash into Mars
Phobos, will crash into Mars
 Europa, moon of Jupiter
Europa, moon of Jupiter
 Io, moon of Jupiter
Io, moon of Jupiter
 Iapetus, moon of Saturn
Iapetus, moon of Saturn
 Dione, moon of Saturn
Dione, moon of Saturn
 Mimas, moon of Saturn
Mimas, moon of Saturn
 Impact theory at the origin of the Moon
Impact theory at the origin of the Moon
 Neptune's moons
Neptune's moons
 Lunar Eclipse, Celestial Concordance
Lunar Eclipse, Celestial Concordance
 Pluto and its satellites
Pluto and its satellites
 The Large Craters of the Moon
The Large Craters of the Moon
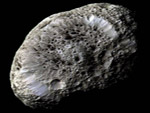 Hyperion, moon of Saturn
Hyperion, moon of Saturn
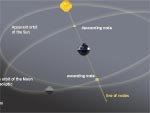 Eclipses explained by the plane of the lunar orbit
Eclipses explained by the plane of the lunar orbit
 Titan and Dione seen by cassini
Titan and Dione seen by cassini
 Eruptions of ice geysers on Enceladus
Eruptions of ice geysers on Enceladus
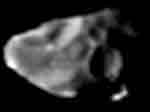 Amalthea, a block remnant of Jupiter
Amalthea, a block remnant of Jupiter
 Deimos, moon of Mars
Deimos, moon of Mars
 Illusion of the Big Moon
Illusion of the Big Moon
 Little Rhea, very close to Saturn
Little Rhea, very close to Saturn
 Helen, the small Trojan moon of Saturn
Helen, the small Trojan moon of Saturn
 Titania, moon of Uranus
Titania, moon of Uranus
 The Blue Moon
The Blue Moon
 Stickney Crater on Phobos
Stickney Crater on Phobos
 Charon the great moon of Pluto
Charon the great moon of Pluto
 Roche limit or limit not to be exceeded
Roche limit or limit not to be exceeded
 Super Moon
Super Moon
 The moons of the solar system
The moons of the solar system
 Ganymede, Jupiter's largest moon
Ganymede, Jupiter's largest moon
 Tethys, Moon of Saturn
Tethys, Moon of Saturn
 Titan, moon of Saturn
Titan, moon of Saturn
 2 new moons for Jupiter
2 new moons for Jupiter
 Prometheus, the shepherd satellite of Saturn
Prometheus, the shepherd satellite of Saturn
 Triton, Neptune's largest moon
Triton, Neptune's largest moon
 Miranda, moon of Uranus
Miranda, moon of Uranus
 Transit of the Moon in front of the Sun
Transit of the Moon in front of the Sun
 The mascons or gravitational anomalies of the Moon
The mascons or gravitational anomalies of the Moon