Definition of the entropy | ||||
What the entropy? |  Automatic translation Automatic translation | Updated June 01, 2013 | ||
Entropy is related to the notions of order and microscopic disorder and specifically the transition from a disordered state to a more disordered state. A state is more disordered it may take many different microscopic states. The entropy, of Greek 'review', is a function thermodynamics. In thermodynamics, the entropy is a function of state (pressure, temperature, volume, quantity of matter) Introduced in the middle of the 19th century by Clausius within the framework of the second principle, according to the works of Carnot. Clausius introduced this greatness to characterize mathematically the irreversibility of physical processes such as a working transformation in heat. He showed that the relationship Q/T (where Q is the quantity of heat exchanged by a system in the temperature T) corresponds, in classic thermodynamics, to the variation of a function of state which it called entropy S and the unit of which is the joule by kelvin ( J/K). The unit of entropy, the Joule by Kelvin corresponds to the quantity of entropy won by a system which receives 1 joule of heat by Kelvin. Thrown in a turbine, the water of a dam transforms its gravitational energy into electrical energy, later, we shall make a movement in an electric engine or of the heat in a radiator. | Throughout these transformations, the energy degrades, in other words, its entropy increases. A cup which breaks itself never returns behind, a body which dies will not live again any more. The total entropy of an isolated system always has to increase, its disorder always has to grow, it is the second principle of the thermodynamics. Originally, the entropy indicates the phenomenon of the thermal exchange which equalizes the temperatures or the waste of the energy in heat, but it is a more general law and which is not so easy to interpret. It is even difficult to understand the concept energy, this greatness which for an isolated system, has the property to keep till mists of time. |  Image: The files of a hard disk are also a demonstration of the entropy, they will never find the order of the departure. | ||
Order or disorder | ||||
The statistical thermodynamics then supplied a new orientation in this abstract physical greatness. It is going to measure the degree of disorder of a system at the tiny level. The more the entropy of the system is raised, the less its elements are ordered, bound between them, capable of producing mechanical effects, and bigger is the part of the energy unused or used in a inconsistent way. Ludwig Eduard Boltzmann (1844 − 1906) formulated a mathematical expression of the statistical entropy according to the number of tiny states Ω defining the state of balance of a system given to the macroscopic level. | In this example the number of tiny configurations (thus the entropy) is indeed a measure of the disorder. If this notion of disorder is often subjective, the number Ω of configurations is him, objective because it is a number. | 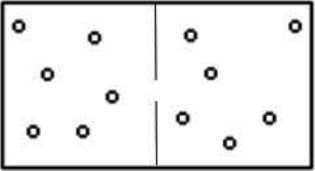 Image: The possibility to find all the molecules of the same side of the container so as to leave half of the void volume is low compared to immensely greater opportunities for which the molecules are uniformly distributed throughout the volume. Thus a thermodynamic equilibrium occurs when the system has the maximum entropy value. The entropy is defined by the Boltzmann formula, S = k log W. | ||
Some examples of entropy | ||||
Both expressions of the entropy result simply from two different points of view, as we consider the system thermodynamics at the macroscopic level or at the tiny level. | In a liquid the mutual distances are smaller and molecules are less free. In solid one every molecule is connected elastically to its neighbors and vibrates around a fixed average position. The energy of every particle is unpredictable. | Image: Entropy, uncertainty, disorder, complexity, thus appear as adversities of the same concept. Under the one or other one of these forms, the entropy is associated with the notion of probability. |
"The data available on this site may be used provided that the source is duly acknowledged."



 Feynman diagrams and particle physics
Feynman diagrams and particle physics
 Stars cannot create elements heavier than iron because of the nuclear instability barrier
Stars cannot create elements heavier than iron because of the nuclear instability barrier
 What is β radioactivity?
What is β radioactivity?
 Planck wall theory
Planck wall theory
 Is emptiness really empty?
Is emptiness really empty?
 The Large Hadron Collider
The Large Hadron Collider
 The hadron is not a fixed object
The hadron is not a fixed object
 Radioactivity, natural and artificial
Radioactivity, natural and artificial
 The scale of nanoparticles
The scale of nanoparticles
 Schrodinger's Cat
Schrodinger's Cat
 Before the big bang the multiverse
Before the big bang the multiverse
 Eternal inflation
Eternal inflation
 Gravitational waves
Gravitational waves
 Principle of absorption and emission of a photon
Principle of absorption and emission of a photon
 Beyond our senses
Beyond our senses
 What is a wave?
What is a wave?
 The fields of reality: what is a field?
The fields of reality: what is a field?
 Space in time
Space in time
 Quantum computers
Quantum computers
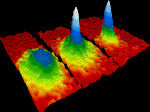 Bose-Einstein condensate
Bose-Einstein condensate
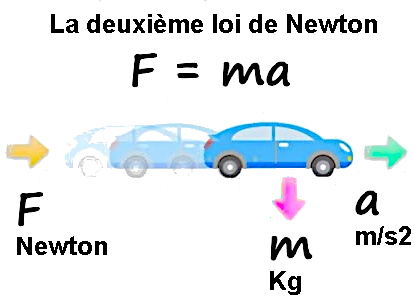 Equation of Newton's three laws
Equation of Newton's three laws
 Field concept in physics
Field concept in physics
 The electron, a kind of electrical point
The electron, a kind of electrical point
 Entropy and disorder
Entropy and disorder
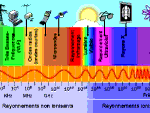 Light, all the light of the spectrum
Light, all the light of the spectrum
 The infernal journey of the photon
The infernal journey of the photon
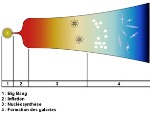 Mystery of the Big Bang, the problem of the horizon
Mystery of the Big Bang, the problem of the horizon
 The neutrino and beta radioactivity
The neutrino and beta radioactivity
 Einstein's space time
Einstein's space time
 The incredible precision of the second
The incredible precision of the second
 Why does physics have constants?
Why does physics have constants?
 Spectroscopy, an inexhaustible source of information
Spectroscopy, an inexhaustible source of information
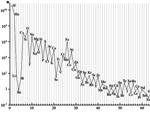 Abundance of chemical elements in the universe
Abundance of chemical elements in the universe
 Effects of light aberration
Effects of light aberration
 The size of atoms
The size of atoms
 The magnetic order and magnetization
The magnetic order and magnetization
 The quark confinement
The quark confinement
 Superpositions of quantum states
Superpositions of quantum states
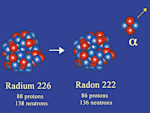 Alpha decay (α)
Alpha decay (α)
 Electromagnetic induction equation
Electromagnetic induction equation
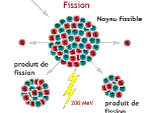 Nuclear fusion, natural energy source
Nuclear fusion, natural energy source
 Does dark matter exist?
Does dark matter exist?
 Non-baryonic matter
Non-baryonic matter
 The mystery of the structure of the atom
The mystery of the structure of the atom
 The mystery of matter, where mass comes from
The mystery of matter, where mass comes from
 Nuclear energy and uranium
Nuclear energy and uranium
 The Universe of X-rays
The Universe of X-rays
 How many photons to heat a coffee?
How many photons to heat a coffee?
 Image of gold atom, scanning tunneling microscope
Image of gold atom, scanning tunneling microscope
 Quantum tunneling of quantum mechanics
Quantum tunneling of quantum mechanics
 Entropy and its effects, the passage of time
Entropy and its effects, the passage of time
 The 12 particles of matter
The 12 particles of matter
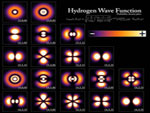 The atomic orbital or image atom
The atomic orbital or image atom
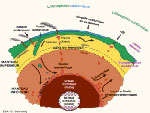 Earth's radioactivity
Earth's radioactivity
 The Leap Second
The Leap Second
 The vacuum has considerable energy
The vacuum has considerable energy
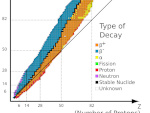 The valley of stability of atomic nuclei
The valley of stability of atomic nuclei
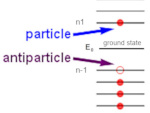 Antimatter and antiparticle
Antimatter and antiparticle
 What is an electric charge?
What is an electric charge?
 Our matter is not quantum!
Our matter is not quantum!
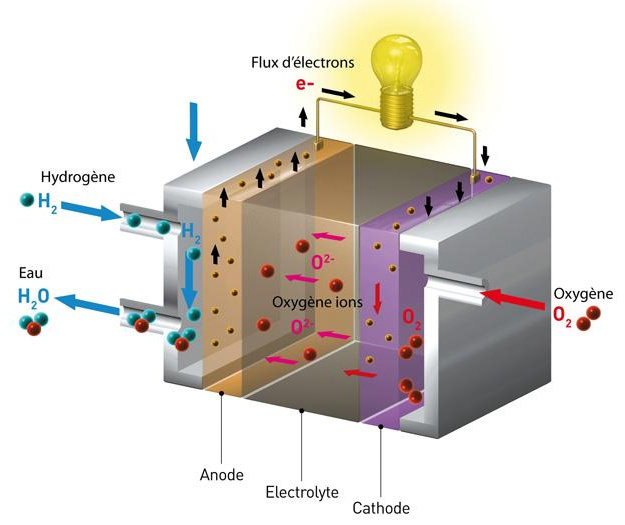 Why use hydrogen in the fuel cell?
Why use hydrogen in the fuel cell?
 The secrets of gravity
The secrets of gravity
 E=mc2 explains the mass of the proton
E=mc2 explains the mass of the proton
 Image of gravity since Albert Einstein
Image of gravity since Albert Einstein
 Einstein's miraculous year: 1905
Einstein's miraculous year: 1905
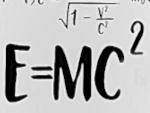 What does the equation E=mc2 really mean?
What does the equation E=mc2 really mean?
 Special relativity and space and time
Special relativity and space and time