Last updated July 23, 2024

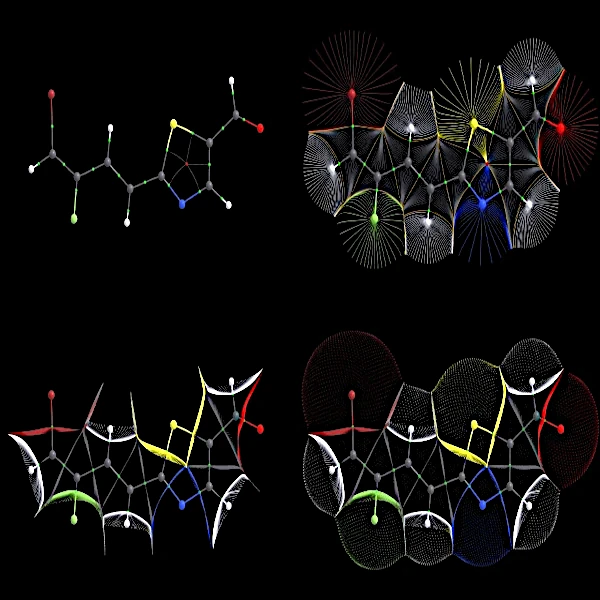
Quantum Field Theory: Everything is Fields

Image description: This representation of the molecular wave function shows the boundary of atoms in a molecule. Where does one atom begin and another end? An atom is a field, and it is the field lines that define its volume. No one has ever seen the fields of quantum physics, but they might look like this computer image. When atoms bond, their fields deform, and this deformation characterizes the bonds. The particles of quantum theory are not "little balls" but undulations, fields that possess a wavelength. This wavelength represents the size of the particle, and the field represents its energy. Image credit: T.A. Keith.

The Fields of Reality

Introduction to Quantum Field Theory

When discussing matter and its behavior in the infinitely small world of particles, we enter the realm of quantum field theory. Quantum field theory helps us understand particle physics. In certain situations, the number of particles entering a spacetime region fluctuates and differs from the number exiting.
The number of particles changes when, for example, an atom in an initial state produces an atom plus 1 photon in a final state. In other words, a photon suddenly emerges from the vacuum and appears in the electromagnetic field. Quantum theory tells us that in the real world, everything is a "field."

Fields: The Energy Carriers of the Universe

We are entirely immersed, down to our deepest selves, in multiple fields with astonishing characteristics. The field is a fundamental concept in physics; it is not made of anything else—it constitutes the real world itself. Fields carry the energy of everything that exists in the universe, from atoms to large galactic structures.
Magnetism, gravity, nuclear force, light, matter, and many other physical phenomena are carried by fields. The most surprising thing is that matter itself, of which we are made, consists of a set of fields. Electrons and protons are also fields, so we are made of fields that defy intuition.
In other words, we are made of an aggregate of ghostly quantum particles bathing in fields. These fields carry the energy of particles throughout all available space around them.

Interactions and Particles in Fields

With the concept of fields, our understanding of the nature of things is revolutionary—reality becomes strange and escapes our five main senses. Reality is not simply explained by the presence of matter but also by exchanges and interactions between real objects and virtual objects in low-energy quantum fields.
In the quantum world, all particles of the Standard Model—fermions and bosons—emerge from vibrations in a field. This is, in fact, the basic concept behind particle accelerators like the Large Hadron Collider (LHC). When scientists want to observe a particle, they cause collisions with energy corresponding to that particle.
Quarks and electrons make up ordinary matter, but matter above absolute zero (-273.15°C) emits radiation, i.e., light that moves through a field. Each type of fermion and boson has its own field. Particles are considered excited states of these fields.

The Wave-Particle Duality and Intuition

The "wave-particle duality" of light was extended to electrons in 1929 by the French mathematician and physicist Louis de Broglie (1892–1987) and later to all particles. However, our minds need images of our world to feed intuition and represent concepts.
But conceptualizing quantum mechanics and the set of quantum fields in which we exist is not easy. Everything is a "field," yet quantum fields—dynamic, charged, bubbling systems—are all subsets of either the gravitational field or the electromagnetic field, the only two fundamental fields of nature.

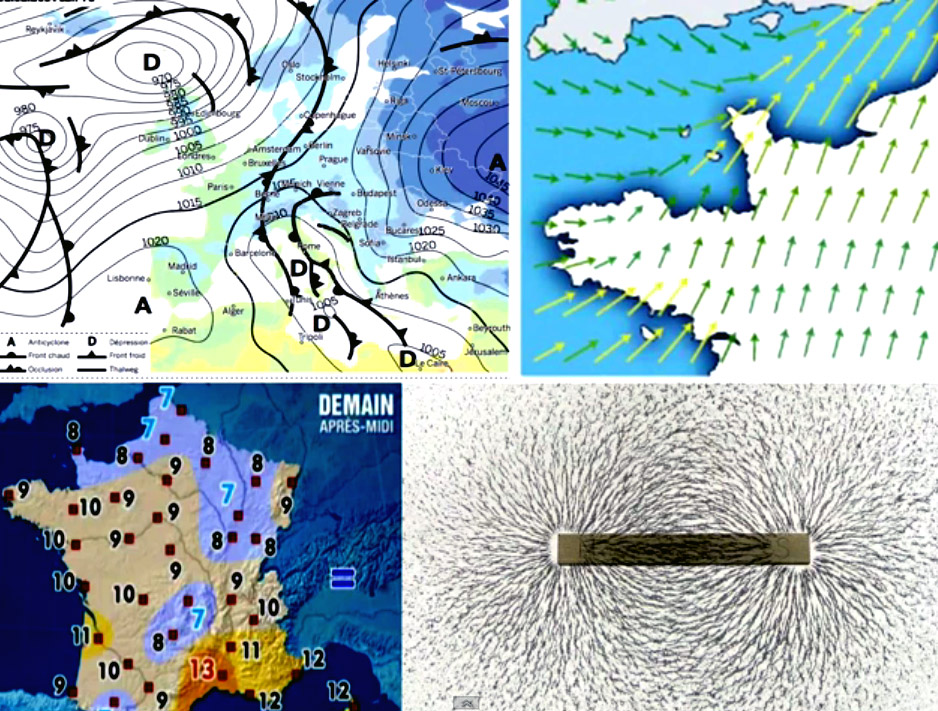
Image description: A field cannot be represented by an image, but it can be mapped.

What is a Field?

General Definition

In physics, a field consists of three linked things in a system with many objects: A defined portion of space, a measurable physical quantity, and a relationship linking the space portion to the physical quantity. In other words, a field is filled with physical quantities—measurable, quantifiable objects using an instrument—where each point in space is linked to the physical quantity by a correspondence or function. For example, atmospheric pressure, air temperature, wind speed, rain, magnetism, gravity, and radioactivity can all be represented by fields.

Scalar and Vector Fields

Fields are scalar or vectorial.
A scalar field is measurable by a single quantity. For example, temperature or mass is defined by a physical quantity fully measurable by a single value.
A vector field is associated with a vector quantity, meaning a single value is insufficient. Direction and sense (like in a wind speed field) are also required.

Representation and Energy of Fields

How to represent a field?
For a scalar field, represent spaces where the value is identical, as in temperature or pressure fields (see 1st and 3rd images).
For a vector field, represent field lines where each point is a tangent field vector, like in wind direction or magnetic fields (see 2nd and 4th images).
The field's energy fades in space. That’s why, outside the electromagnetic field generated by a radio station, we no longer receive signals. When an electromagnetic field is abruptly interrupted, a spark occurs (the field indeed contains energy).

The Quantum Field

In quantum physics, the notion of a corpuscle is not used because quantum particles are not corpuscles but mathematical quantities represented by state vectors in Hilbert space. This concept defies intuition and our vision.

The quantum field fills all space. It is a vector field of subatomic particles, whose quantity is quantized (taken from a finite set of values), and the relationship is a wave function (state vector). This allows knowing all the system's information and gives every particle the interference properties typical of a wave.
In the quantum world, all particles in their ground state (non-excited) are waves.
A hadron field consists of virtual particles—partons (gluons and quarks)—that stir, appearing and disappearing in empty space.
A field carried by the weak nuclear force is traversed by W and Z bosons.
An electromagnetic field is traversed by photons.
A gravitational field is traversed by "gravitons" (not yet discovered), as gravity is a very weak force.
Thus, virtual and real particles of matter bathe in these bubbling fields, occasionally transferring energy. This is what scientists induce in a collider. In a collider, when an electron and a positron meet, they annihilate and transfer their energy to the vacuum’s buzz. This energy creates real material particles that emerge from the vacuum and appear briefly on computer screens.

Energy and Frequency of a Field

A field is thus a bubbling system occupying all space—an undulation, vibration, oscillation, a wave with a wavelength and thus a frequency.
Thanks to Max Planck’s (1858–1947) formula e=hν, a field also has energy (e is the energy of something moving, h is Planck’s constant, and ν (nu) is frequency). This pair of values—energy and frequency—characterizes the field at every point in space. Each point in space allows the emergence or annihilation of particles.