À quelle distance se trouve l’horizon ?

Comprendre la distance apparente de l'horizon

L’horizon est la limite apparente entre la Terre et le ciel. Sa distance dépend de la courbure terrestre, de la hauteur de l’observateur et de la réfraction atmosphérique. Cette distance peut être calculée à l'aide d'une formule géométrique simple sans prendre en compte la réfraction atmosphérique.

Distance géométrique simple de l'horizon

La distance à l’horizon, sur une Terre idéale parfaitement sphérique et sans atmosphère, se calcule par \(\,d = \sqrt{2Rh + h^2}\,\) où \(R\) est le rayon terrestre (\(\approx 6371\) km) et \(h\) la hauteur de l’observateur. Par exemple, à 2 m de hauteur, l’horizon géométrique se trouve à environ 5 km.

Calcul détaillé de la distance de l'horizon

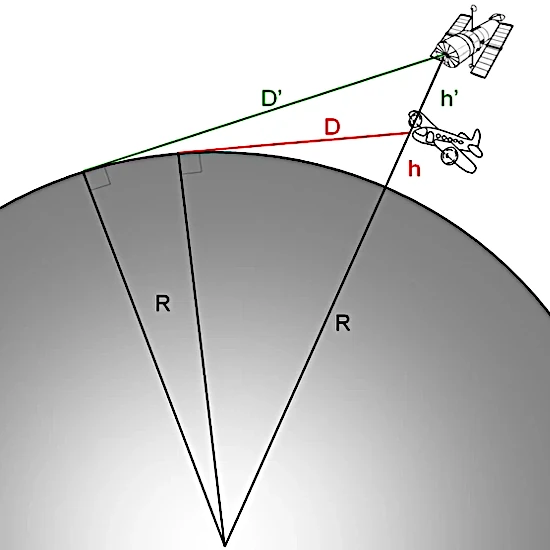
Considérons un observateur situé à une hauteur \(h\) au-dessus de la surface terrestre. Soit \(R\) le rayon moyen de la Terre (\(R \approx 6371\) km). La droite reliant l’œil de l’observateur au point de tangence sur la surface est perpendiculaire au rayon terrestre à ce point. Le triangle formé par le centre de la Terre, le point de tangence et l’observateur est rectangle. En appliquant le théorème de Pythagore : \( (R + h)^2 = R^2 + d^2 \) où \(d\) est la distance en ligne droite entre l’observateur et l’horizon. La distance au sol, suivant la courbure, est : \( s = R \cdot \theta \) avec \(\theta = \arccos\left( \frac{R}{R+h} \right)\). En combinant : \( s = R \cdot \arccos\left( \frac{R}{R+h} \right) \) et pour \(h \ll R\), on obtient l’approximation : \( s \approx \sqrt{2Rh + h^2} \)

Calcul de la distance de l'horizon avec la correction atmosphérique

En réalité, la réfraction atmosphérique augmente légèrement cette distance car les rayons lumineux sont courbés vers le sol. En conditions standard, on modélise cet effet en remplaçant \(R\) par \(R / (1 - k)\) avec \(k \approx 0{,}13\).

Tableau comparatif des distances de l'horizon en fonction de l'altitude

N.B. : L’horizon terrestre n’existe jamais complètement à partir du moment où l’on quitte la surface : plus on monte, plus la portion visible de la Terre s’agrandit. Depuis l’ISS (408 km), on aperçoit environ 3,2 % de la surface totale (≈9 millions de km²). En orbite géostationnaire (36 000 km), on voit exactement la moitié de la planète. Pour observer 99 % de la surface en un seul coup d’œil, il faudrait atteindre environ 21 700 km d’altitude. Au-delà, l’horizon recule pratiquement jusqu’au bord opposé de la Terre, mais il ne disparaît totalement qu’à distance infinie.